网易2018校园招聘编程题真题集合（二）

发表于 | 分类于 | ℃
字数统计: 2,558 字 | 阅读时长 ≈ 11 分钟

继续第二期，这部分的三道题变得比较复杂了。

Qus4 游历魔法王国

试题描述

魔法王国一共有n个城市,编号为0~n-1号,n个城市之间的道路连接起来恰好构成一棵树。
小易现在在0号城市,每次行动小易会从当前所在的城市走到与其相邻的一个城市,小易最多能行动L次。
如果小易到达过某个城市就视为小易游历过这个城市了,小易现在要制定好的旅游计划使他能游历最多的城市,请你帮他计算一下他最多能游历过多少个城市(注意0号城市已经游历了,游历过的城市不重复计算)。

输入描述:

输入包括两行,第一行包括两个正整数n(2 ≤ n ≤ 50)和L(1 ≤ L ≤ 100),表示城市个数和小易能行动的次数。
第二行包括n-1个整数parenti, 对于每个合法的i(0 ≤ i ≤ n - 2),在(i+1)号城市和parent[i]间有一条道路连接。

输出描述:

输出一个整数,表示小易最多能游历的城市数量。

示例1

输入

5 2
0 1 2 3

输出

3

试题分析

试题最后抽象成求树的最大深度。
输入描述中第二行 第二行包括n-1个整数parent[i](0 ≤ parent[i] ≤ i), 对于每个合法的i(0 ≤ i ≤ n - 2),在(i+1)号城市和parent[i]间有一条道路连接，绕了半天，其实是描述树的形状。
例如测试用例：

10 10
0 3 1 3 0 5 2 7 5

对应的关系如下：

Tables Col 1 Col 2 Col 3 Col 4 Col 5 Col 6 Col 7 Col 8 Col 9
子节点(i) 1 2 3 4 5 6 7 8 9
父节点(parent[i]) 0 3 1 3 0 5 2 7 5

生成的树：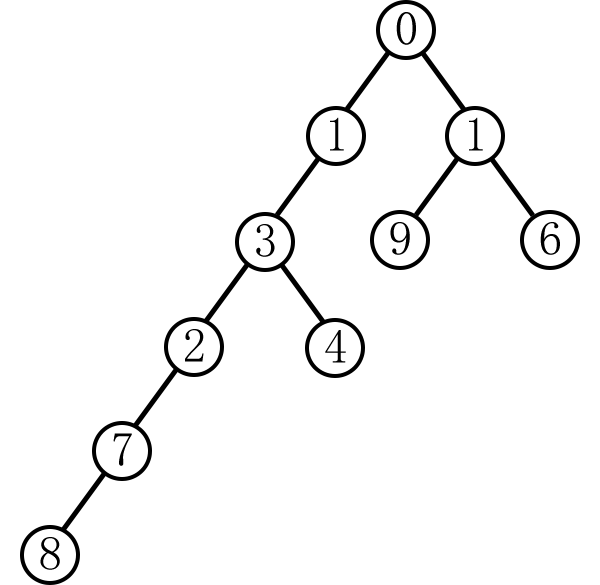

树的结构有了之后，就只需要根据树的最大深度depth与可走的最大步数L之间的关系来判断最终的游历城市数量。

  1. 当depth ≥ L时，那么能够游历的城市数即L + 1（因为出发位置在得0号城市，算是已经游历的城市）；
  2. 当depth < L时，即需要走重复的路。显而易见，返回需要走两遍相同的路径。最优化的行走方案是将旅程分为两个部分，一个部分为走到最大深度depth，另一部分为走重复路的短路径(L-depth)/2（即除了树的大深度外的步数，由于折返故除以2）。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
function main(argument) {
    var n = argument[0].split(' ')[0];
    var l = parseInt(argument[0].split(' ')[1]);
    var parents = argument[1].split(' ');
    var depth = [];
    var tempArray = [];
    depth[0] = 0;
    for (var i = 1; i < n; i++) {
        if (typeof(depth[parents[i - 1]]) !== "undefined") {
            depth[i] = depth[parents[i - 1]] + 1;
        } else {
            tempArray.push(i);
        }
    }
    if (tempArray.length) {
        for (i = 0; i < tempArray.length; i++) {
            depth[tempArray[i]] = depth[parents[tempArray[i] - 1]] + 1;
        }
    }
    var max = Math.max(...depth);
    if (max >= l) {
        return l + 1;
    } else {
        return parseInt((l - max) / 2) + max + 1;
    }
}
var lines = [];
while (line = readline()) {
    lines.push(line);
}
print(main(lines));

反思

  1. 代码中有一项未判断，即当步数L>(depth + (L-depth)/2)时，部署应该为城市数n;
  2. 在生成树的过程中，由于遍历过程中可能部分节点在未生成时引用会出现undefined问题，故引入判断，在第15行处再循环一次；
  3. 第20行处实用了ES6中的扩展运算符（ ... ），在学习ES6时再继续详细解答；
  4. 其实对于生成树与计算最大深度还是不太明白，该抽时间补一补数据结构了。

Qus5 重排数列

试题描述

小易有一个长度为N的正整数数列A = {A[1], A[2], A[3]..., A[N]}。
牛博士给小易出了一个难题:
对数列A进行重新排列,使数列A满足所有的A[i] * A[i + 1](1 ≤ i ≤ N - 1)都是4的倍数。
小易现在需要判断一个数列是否可以重排之后满足牛博士的要求。

输入描述:

输入的第一行为数列的个数t(1 ≤ t ≤ 10),
接下来每两行描述一个数列A,第一行为数列长度n(1 ≤ n ≤ 10^5)
第二行为n个正整数A[i](1 ≤ A[i] ≤ 10^9)

输出描述:

对于每个数列输出一行表示是否可以满足牛博士要求,如果可以输出Yes,否则输出No。

示例1

输入

2
3
1 10 100
4
1 2 3 4

输出

Yes
No

试题分析

根据题意，将数列A中的数字分为三类：

n4 : 可以被4整除的数
n2 : 可以被2整除但不可以被4整除的数
n1 : 不可以被2整除的数

那么如果要满足题目要求即A[i] * A[i + 1](1 ≤ i ≤ N - 1)都是4的倍数，则必须以下两种情况：

  1. 数字n1的两侧都要有n4（数列第一个或最后一个只需满足一侧存在n4即可）；
  2. 数字n2的两侧要存在n2或者n4；

那么对条件进行简化，数组A可能出现的情况：

  1. n4 > = n1 —— 满足题目要求；
  2. n4 = n1 - 1 && n4 + n1 = A.length —— 数列第一个与最后一个均为n1,满足题目要求；
  3. n4 < n1 - 1 —— 不满足

这样就很清晰了，详情见代码实现

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
function main(argument) {
    var tarArray = [],
        resultArray = [],
        n4 = 0,
        n1 = 0;
    for (var i = 2; i < argument.length;) {
        tarArray.push(argument[i]);
        i = i + 2;
    }

    for (i = 0; i < tarArray.length; i++) {
        var _ta = tarArray[i].split(" ");
        n4 = num_mod({
            ta: _ta
        });
        n1 = num_mod({
            ta: _ta,
            mod: 2,
            rtnMod: false
        });

        if (n4 >= n1 || (n4 >= n1 - 1 && (n4 + n1) === _ta.length)) {
            resultArray.push("Yes");
        } else {
            resultArray.push("No");
        }
    }

    return resultArray;

}

function num_mod(argument) {
    var deal_arr = argument.ta; //目标数组
    var _mod = typeof(argument.mod) === "undefined" ? 4 : argument.mod; //取模的被除数 默认为4
    var _rtnMod = typeof(argument.rtnMod) === "undefined" ? true : argument.rtnMod; //返回值 默认为true true/取模后为0的个数 false/取模后不为0的个数

    var _rtn = 0;

    for (var i = 0; i < deal_arr.length; i++) {
        if (deal_arr[i] % _mod === 0) {
            _rtn = _rtn + 1;
        }
    }

    return _rtnMod ? _rtn : (deal_arr.length - _rtn);
}

var lines = [];
while (line = readline()) {
    lines.push(line);
}
print(main(lines).join("\n"));

反思

  1. 最开始的思路是按照题意，数列中的所有数字互相相乘，得出新的数列。判断新的数列中的数组是否能被4整除，如果得到的结果大于原数组length - 1 即满足条件，这样能通过最开始的两组数列的测验，因为开始的数列相对比较短（4个以下）;
  2. 写了一个取模的函数，参数采用json格式；

Qus6 最长公共子括号序列

试题描述

一个合法的括号匹配序列被定义为:

  1. 空串""是合法的括号序列
  2. 如果"X"和"Y"是合法的序列,那么"XY"也是一个合法的括号序列
  3. 如果"X"是一个合法的序列,那么"(X)"也是一个合法的括号序列
  4. 每个合法的括号序列都可以由上面的规则生成

例如"","()", "()()()", "(()())", "(((()))"都是合法的。
从一个字符串S中移除零个或者多个字符得到的序列称为S的子序列。
例如"abcde"的子序列有"abe","","abcde"等。
定义LCS(S,T)为字符串S和字符串T最长公共子序列的长度,即一个最长的序列W既是S的子序列也是T的子序列的长度。
小易给出一个合法的括号匹配序列S,小易希望你能找出具有以下特征的括号序列t:

  1. T跟S不同,但是长度相同
  2. T也是一个合法的括号匹配序列
  3. LCS(S, T)是满足上述两个条件的T中最大的

因为这样的T可能存在多个,小易需要你计算出满足条件的T有多少个。

如样例所示: S = "(())()",跟字符串S长度相同的合法括号匹配序列有:
"()(())", "((()))", "()()()", "(()())",其中LCS( "(())()", "()(())" )为4,其他三个都为5,所以输出3.

输入描述:

输入包括字符串S(4 ≤ |S| ≤ 50,|S|表示字符串长度),保证S是一个合法的括号匹配序列。

输出描述:

输出一个正整数,满足条件的T的个数。

示例1

输入

(())()

输出

3

试题分析

很容易得出满足LCS(S , T)最大的S与T最长序列W的长度为S.length - 1。那么接下来的问题就很容易处理了。
将S中的任意一个字节抽离出来放到任意一个位置生成新的字符串T，通过合法性判断与去重，并且去除原字符串，得到的数组长度即为最终结果。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
function main(str) {
    var strArray = [];
    var _ins = "",
        _other = "";

    for (var i = 0; i < str.length; i++) {
        _ins = str[i];
        _other = str.substring(0, i) + str.substring(i + 1, str.length);
        for (var j = 0; j < _other.length; j++) {
            var _temp_str = _other.substring(0, j) + _ins + _other.substring(j, _other.length);
            if (is_mate(_temp_str)) {
                strArray.push(_temp_str);
            }
        }
    }
    return arr_unique(strArray).length - 1;
}

function arr_unique(arr) {
    arr.sort();
    var res = [arr[0]];
    for (var i = 1; i < arr.length; i++) {
        if (arr[i] !== res[res.length - 1]) {
            res.push(arr[i]);
        }
    }
    return res;
}

function is_mate(str) {
    var _arr = [],
        _rtn = true;
    for (var i = 0; i < str.length; i++) {
        if (str[i] === "(") {
            _arr.push(str[i])
        } else if (str[i] === ")") {
            if (typeof(_arr.pop()) === "undefined") {
                _rtn = false;
                break;
            }
        }
    }
    if (_arr.length !== 0) {
        _rtn = false;
    }
    return _rtn;
}
while (line = readline()) {
    var lines = line.split(" ")[0];
    print(main(lines));
}

反思

  1. 通过数组的堆栈方式来判断括号字符串是否合法，主要通过出栈方法array.pop()方法是否为空来判断（代码37行）；
  2. 因为经过遍历去重后的数组，肯定有一个和原数组一样，所以返回最终结果时不需要再对原数组进行去重处理，直接将返回的length - 1即最后结果（代码37行）;
  3. 第10行的时候，犯了个低级错误，写错变量名，调试了很久才发现。。